机器学习——降维

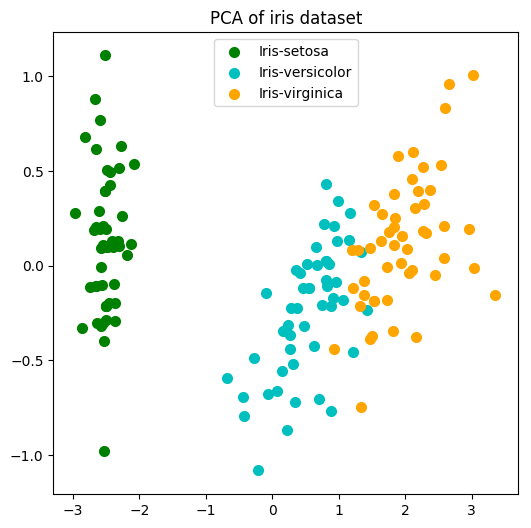
实战演练 —— 降维

3.4 PCA实现

任务介绍：

  • 请使用Numpy实现PCA，定义为一个函数pca()

  • 函数包含两个参数：dataMat数据矩阵和n_components低维维数，并返回在新空间下的数据矩阵lowdMat和转换矩阵tfMat

  • 现已经读取鸢尾花数据iris.csv得到iris，请利用自定义pca()将数据从四维降到二维空间，得到最终的低维数据矩阵iris2d

预期实验结果

部分截图如下：

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import pandas as pd
import numpy as np
from numpy import linalg as LA

# 读取数据
iris = pd.read_csv('iris.csv', usecols=range(4))

# 定义主成分分析函数
def pca(dataMat, n_components):
    
    # 数据中心化
    meanVals = np.mean(dataMat, axis=0)
    centered = dataMat-meanVals
    # 计算协方差矩阵，并进行特征值分解
    # 注意，协方差矩阵计算需指定rowvar参数为False，即表明每一列
    # 为每一个特征的不同取值
    covMat =  np.cov(centered, rowvar=False)
    w, v = LA.eig(covMat)
    
    # 将特征值从大到小排序，并得到对应的索引值序列
    idxMin2Max = np.argsort(w)
    idxMax2Min = idxMin2Max[::-1]

    # 取前n_components个特征向量构成转换矩阵
    vidx = idxMax2Min[:n_components]
    tfMat = v[:,vidx]

    # 将原始数据转换到新的低维空间
    lowdMat =  np.matmul(centered, tfMat)
    return lowdMat, tfMat

# 使用自定义pca函数对鸢尾花数据进行降维
irisMat = np.mat(iris)
iris2d, _ = pca(irisMat,2)
print(iris2d)

# 请直接运行处结果，然后提交作业，该运行结果会自动一同提交上去
[[-2.68420713 -0.32660731]
 [-2.71539062  0.16955685]
 [-2.88981954  0.13734561]
 [-2.7464372   0.31112432]
 [-2.72859298 -0.33392456]
 [-2.27989736 -0.74778271]
 [-2.82089068  0.08210451]
 [-2.62648199 -0.17040535]
 [-2.88795857  0.57079803]
 [-2.67384469  0.1066917 ]
 [-2.50652679 -0.65193501]
 [-2.61314272 -0.02152063]
 [-2.78743398  0.22774019]
 [-3.22520045  0.50327991]
 [-2.64354322 -1.1861949 ]
 [-2.38386932 -1.34475434]
 [-2.6225262  -0.81808967]
 [-2.64832273 -0.31913667]
 [-2.19907796 -0.87924409]
 [-2.58734619 -0.52047364]
 [-2.3105317  -0.39786782]
 [-2.54323491 -0.44003175]
 [-3.21585769 -0.14161557]
 [-2.30312854 -0.10552268]
 [-2.35617109  0.03120959]
 [-2.50791723  0.13905634]
 [-2.469056   -0.13788731]
 [-2.56239095 -0.37468456]
 [-2.63982127 -0.31929007]
 [-2.63284791  0.19007583]
 [-2.58846205  0.19739308]
 [-2.41007734 -0.41808001]
 [-2.64763667 -0.81998263]
 [-2.59715948 -1.10002193]
 [-2.67384469  0.1066917 ]
 [-2.86699985 -0.0771931 ]
 [-2.62522846 -0.60680001]
 [-2.67384469  0.1066917 ]
 [-2.98184266  0.48025005]
 [-2.59032303 -0.23605934]
 [-2.77013891 -0.27105942]
 [-2.85221108  0.93286537]
 [-2.99829644  0.33430757]
 [-2.4055141  -0.19591726]
 [-2.20883295 -0.44269603]
 [-2.71566519  0.24268148]
 [-2.53757337 -0.51036755]
 [-2.8403213   0.22057634]
 [-2.54268576 -0.58628103]
 [-2.70391231 -0.11501085]
 [ 1.28479459 -0.68543919]
 [ 0.93241075 -0.31919809]
 [ 1.46406132 -0.50418983]
 [ 0.18096721  0.82560394]
 [ 1.08713449 -0.07539039]
 [ 0.64043675  0.41732348]
 [ 1.09522371 -0.28389121]
 [-0.75146714  1.00110751]
 [ 1.04329778 -0.22895691]
 [-0.01019007  0.72057487]
 [-0.5110862   1.26249195]
 [ 0.51109806  0.10228411]
 [ 0.26233576  0.5478933 ]
 [ 0.98404455  0.12436042]
 [-0.174864    0.25181557]
 [ 0.92757294 -0.46823621]
 [ 0.65959279  0.35197629]
 [ 0.23454059  0.33192183]
 [ 0.94236171  0.54182226]
 [ 0.0432464   0.58148945]
 [ 1.11624072  0.08421401]
 [ 0.35678657  0.06682383]
 [ 1.29646885  0.32756152]
 [ 0.92050265  0.18239036]
 [ 0.71400821 -0.15037915]
 [ 0.89964086 -0.32961098]
 [ 1.33104142 -0.24466952]
 [ 1.55739627 -0.26739258]
 [ 0.81245555  0.16233157]
 [-0.30733476  0.36508661]
 [-0.07034289  0.70253793]
 [-0.19188449  0.67749054]
 [ 0.13499495  0.31170964]
 [ 1.37873698  0.42120514]
 [ 0.58727485  0.48328427]
 [ 0.8072055  -0.19505396]
 [ 1.22042897 -0.40803534]
 [ 0.81286779  0.370679  ]
 [ 0.24519516  0.26672804]
 [ 0.16451343  0.67966147]
 [ 0.46303099  0.66952655]
 [ 0.89016045  0.03381244]
 [ 0.22887905  0.40225762]
 [-0.70708128  1.00842476]
 [ 0.35553304  0.50321849]
 [ 0.33112695  0.21118014]
 [ 0.37523823  0.29162202]
 [ 0.64169028 -0.01907118]
 [-0.90846333  0.75156873]
 [ 0.29780791  0.34701652]
 [ 2.53172698  0.01184224]
 [ 1.41407223  0.57492506]
 [ 2.61648461 -0.34193529]
 [ 1.97081495  0.18112569]
 [ 2.34975798  0.04188255]
 [ 3.39687992 -0.54716805]
 [ 0.51938325  1.19135169]
 [ 2.9320051  -0.35237701]
 [ 2.31967279  0.24554817]
 [ 2.91813423 -0.78038063]
 [ 1.66193495 -0.2420384 ]
 [ 1.80234045  0.21615461]
 [ 2.16537886 -0.21528028]
 [ 1.34459422  0.77641543]
 [ 1.5852673   0.53930705]
 [ 1.90474358 -0.11881899]
 [ 1.94924878 -0.04073026]
 [ 3.48876538 -1.17154454]
 [ 3.79468686 -0.25326557]
 [ 1.29832982  0.76101394]
 [ 2.42816726 -0.37678197]
 [ 1.19809737  0.60557896]
 [ 3.49926548 -0.45677347]
 [ 1.38766825  0.20403099]
 [ 2.27585365 -0.33338653]
 [ 2.61419383 -0.55836695]
 [ 1.25762518  0.179137  ]
 [ 1.29066965  0.11642525]
 [ 2.12285398  0.21085488]
 [ 2.3875644  -0.46251925]
 [ 2.84096093 -0.37274259]
 [ 3.2323429  -1.37052404]
 [ 2.15873837  0.21832553]
 [ 1.4431026   0.14380129]
 [ 1.77964011  0.50146479]
 [ 3.07652162 -0.68576444]
 [ 2.14498686 -0.13890661]
 [ 1.90486293 -0.04804751]
 [ 1.16885347  0.1645025 ]
 [ 2.10765373 -0.37148225]
 [ 2.31430339 -0.18260885]
 [ 1.92245088 -0.40927118]
 [ 1.41407223  0.57492506]
 [ 2.56332271 -0.2759745 ]
 [ 2.41939122 -0.30350394]
 [ 1.94401705 -0.18741522]
 [ 1.52566363  0.37502085]
 [ 1.76404594 -0.07851919]
 [ 1.90162908 -0.11587675]
 [ 1.38966613  0.28288671]]

3.5 降维结果分析

任务介绍

  • 我们提前定义好了pca函数pca(dataMat, n_components)，与之前定义的方式不同，现在该函数可以返回低维向量lowdMat、转换矩阵tfMat、特征值w和特征向量v
  • 现有包含590个特征的半导体制造数据集secon，并且我们已经提前对缺失值做了均值填充，可以直接用于降维过程
  • 请使用自定义的pca函数对半导体数据进行降维（假设降维后主成分数目为590个）并分析降维结果
  • 请计算第一主成分(first principal component)方差占总方差的百分比，并存为变量fpc（用于判定本题是否通过）
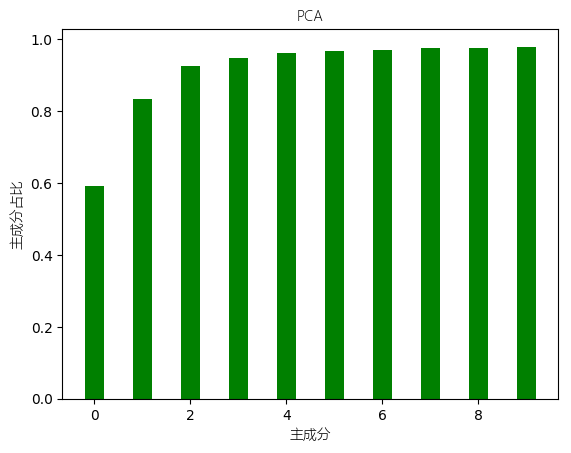
  • 请分析新的低维空间下，每一个主成分对方差的解释占比分别为多少？应该保留多少个主成分？
  • 请尝试绘出累积主成分方差的百分比随主成分数目的变化图？
  • 请尝试计算出重构误差？(提示：通过原始数据与重构数据得到误差矩阵M，并使用LA.norm(M, ‘fro’)计算Frobenius范数)

实验代码

代码1：上一实验中自定义的 pca 函数拷贝至此

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import pandas as pd
import numpy as np
from numpy import linalg as LA

# 读取数据
iris = pd.read_csv('iris.csv', usecols=range(4))
'''
# 定义主成分分析函数
def pca(dataMat, n_components):
    
    # 数据中心化
   # meanVals = dataMat.mean(axis=0)
    meanVals =np.mean(dataMat, axis=0)
    centered = dataMat - meanVals
    
    # 计算协方差矩阵，并进行特征值分解
    # 注意，协方差矩阵计算需指定rowvar参数为False，即表明每一列
    # 为每一个特征的不同取值

    #covMat = centered.T * centered
    covMat = np.cov(centered,rowvar=False)
    w, v = LA.eig(covMat)
    
    # 将特征值从大到小排序，并得到对应的索引值序列
    idxMin2Max = np.argsort(w)
    idxMax2Min = idxMin2Max[::-1]
    
    # 取前n_components个特征向量构成转换矩阵
    vidx = idxMax2Min[:n_components]
    tfMat = v[:, vidx]
    
    # 将原始数据转换到新的低维空间
    lowdMat = np.matmul(dataMat , tfMat)
    
    return lowdMat, tfMat, w, v
'''
# 定义主成分分析函数
def pca(dataMat, n_components):
    
    # 数据中心化
    meanVals = np.mean(dataMat, axis=0)
    centered =  dataMat - meanVals
    
    # 计算协方差矩阵，并进行特征值分解
    # 注意，协方差矩阵计算需指定rowvar参数为False，即表明每一列
    # 为每一个特征的不同取值
    covMat = np.cov(centered, rowvar=False)
    w, v = LA.eig(covMat)
    # 将特征值从大到小排序，并得到对应的索引值序列
    idxMin2Max = np.argsort(w)
    idxMax2Min = idxMin2Max[::-1]
    
    # 取前n_components个特征向量构成转换矩阵
    vidx = idxMax2Min[:n_components]
    tfMat = v[:, vidx]
    
    # 将原始数据转换到新的低维空间
    lowdMat = np.matmul(centered, tfMat)
    return lowdMat, tfMat,w,v

# 使用自定义pca函数对鸢尾花数据进行降维
irisMat = np.mat(iris)
iris2d, _,_,_ = pca(irisMat, n_components=2)

print(iris2d)
[[-2.68420713 -0.32660731]
 [-2.71539062  0.16955685]
 [-2.88981954  0.13734561]
 [-2.7464372   0.31112432]
 [-2.72859298 -0.33392456]
 [-2.27989736 -0.74778271]
 [-2.82089068  0.08210451]
 [-2.62648199 -0.17040535]
 [-2.88795857  0.57079803]
 [-2.67384469  0.1066917 ]
 [-2.50652679 -0.65193501]
 [-2.61314272 -0.02152063]
 [-2.78743398  0.22774019]
 [-3.22520045  0.50327991]
 [-2.64354322 -1.1861949 ]
 [-2.38386932 -1.34475434]
 [-2.6225262  -0.81808967]
 [-2.64832273 -0.31913667]
 [-2.19907796 -0.87924409]
 [-2.58734619 -0.52047364]
 [-2.3105317  -0.39786782]
 [-2.54323491 -0.44003175]
 [-3.21585769 -0.14161557]
 [-2.30312854 -0.10552268]
 [-2.35617109  0.03120959]
 [-2.50791723  0.13905634]
 [-2.469056   -0.13788731]
 [-2.56239095 -0.37468456]
 [-2.63982127 -0.31929007]
 [-2.63284791  0.19007583]
 [-2.58846205  0.19739308]
 [-2.41007734 -0.41808001]
 [-2.64763667 -0.81998263]
 [-2.59715948 -1.10002193]
 [-2.67384469  0.1066917 ]
 [-2.86699985 -0.0771931 ]
 [-2.62522846 -0.60680001]
 [-2.67384469  0.1066917 ]
 [-2.98184266  0.48025005]
 [-2.59032303 -0.23605934]
 [-2.77013891 -0.27105942]
 [-2.85221108  0.93286537]
 [-2.99829644  0.33430757]
 [-2.4055141  -0.19591726]
 [-2.20883295 -0.44269603]
 [-2.71566519  0.24268148]
 [-2.53757337 -0.51036755]
 [-2.8403213   0.22057634]
 [-2.54268576 -0.58628103]
 [-2.70391231 -0.11501085]
 [ 1.28479459 -0.68543919]
 [ 0.93241075 -0.31919809]
 [ 1.46406132 -0.50418983]
 [ 0.18096721  0.82560394]
 [ 1.08713449 -0.07539039]
 [ 0.64043675  0.41732348]
 [ 1.09522371 -0.28389121]
 [-0.75146714  1.00110751]
 [ 1.04329778 -0.22895691]
 [-0.01019007  0.72057487]
 [-0.5110862   1.26249195]
 [ 0.51109806  0.10228411]
 [ 0.26233576  0.5478933 ]
 [ 0.98404455  0.12436042]
 [-0.174864    0.25181557]
 [ 0.92757294 -0.46823621]
 [ 0.65959279  0.35197629]
 [ 0.23454059  0.33192183]
 [ 0.94236171  0.54182226]
 [ 0.0432464   0.58148945]
 [ 1.11624072  0.08421401]
 [ 0.35678657  0.06682383]
 [ 1.29646885  0.32756152]
 [ 0.92050265  0.18239036]
 [ 0.71400821 -0.15037915]
 [ 0.89964086 -0.32961098]
 [ 1.33104142 -0.24466952]
 [ 1.55739627 -0.26739258]
 [ 0.81245555  0.16233157]
 [-0.30733476  0.36508661]
 [-0.07034289  0.70253793]
 [-0.19188449  0.67749054]
 [ 0.13499495  0.31170964]
 [ 1.37873698  0.42120514]
 [ 0.58727485  0.48328427]
 [ 0.8072055  -0.19505396]
 [ 1.22042897 -0.40803534]
 [ 0.81286779  0.370679  ]
 [ 0.24519516  0.26672804]
 [ 0.16451343  0.67966147]
 [ 0.46303099  0.66952655]
 [ 0.89016045  0.03381244]
 [ 0.22887905  0.40225762]
 [-0.70708128  1.00842476]
 [ 0.35553304  0.50321849]
 [ 0.33112695  0.21118014]
 [ 0.37523823  0.29162202]
 [ 0.64169028 -0.01907118]
 [-0.90846333  0.75156873]
 [ 0.29780791  0.34701652]
 [ 2.53172698  0.01184224]
 [ 1.41407223  0.57492506]
 [ 2.61648461 -0.34193529]
 [ 1.97081495  0.18112569]
 [ 2.34975798  0.04188255]
 [ 3.39687992 -0.54716805]
 [ 0.51938325  1.19135169]
 [ 2.9320051  -0.35237701]
 [ 2.31967279  0.24554817]
 [ 2.91813423 -0.78038063]
 [ 1.66193495 -0.2420384 ]
 [ 1.80234045  0.21615461]
 [ 2.16537886 -0.21528028]
 [ 1.34459422  0.77641543]
 [ 1.5852673   0.53930705]
 [ 1.90474358 -0.11881899]
 [ 1.94924878 -0.04073026]
 [ 3.48876538 -1.17154454]
 [ 3.79468686 -0.25326557]
 [ 1.29832982  0.76101394]
 [ 2.42816726 -0.37678197]
 [ 1.19809737  0.60557896]
 [ 3.49926548 -0.45677347]
 [ 1.38766825  0.20403099]
 [ 2.27585365 -0.33338653]
 [ 2.61419383 -0.55836695]
 [ 1.25762518  0.179137  ]
 [ 1.29066965  0.11642525]
 [ 2.12285398  0.21085488]
 [ 2.3875644  -0.46251925]
 [ 2.84096093 -0.37274259]
 [ 3.2323429  -1.37052404]
 [ 2.15873837  0.21832553]
 [ 1.4431026   0.14380129]
 [ 1.77964011  0.50146479]
 [ 3.07652162 -0.68576444]
 [ 2.14498686 -0.13890661]
 [ 1.90486293 -0.04804751]
 [ 1.16885347  0.1645025 ]
 [ 2.10765373 -0.37148225]
 [ 2.31430339 -0.18260885]
 [ 1.92245088 -0.40927118]
 [ 1.41407223  0.57492506]
 [ 2.56332271 -0.2759745 ]
 [ 2.41939122 -0.30350394]
 [ 1.94401705 -0.18741522]
 [ 1.52566363  0.37502085]
 [ 1.76404594 -0.07851919]
 [ 1.90162908 -0.11587675]
 [ 1.38966613  0.28288671]]

代码2：本次实验主要代码

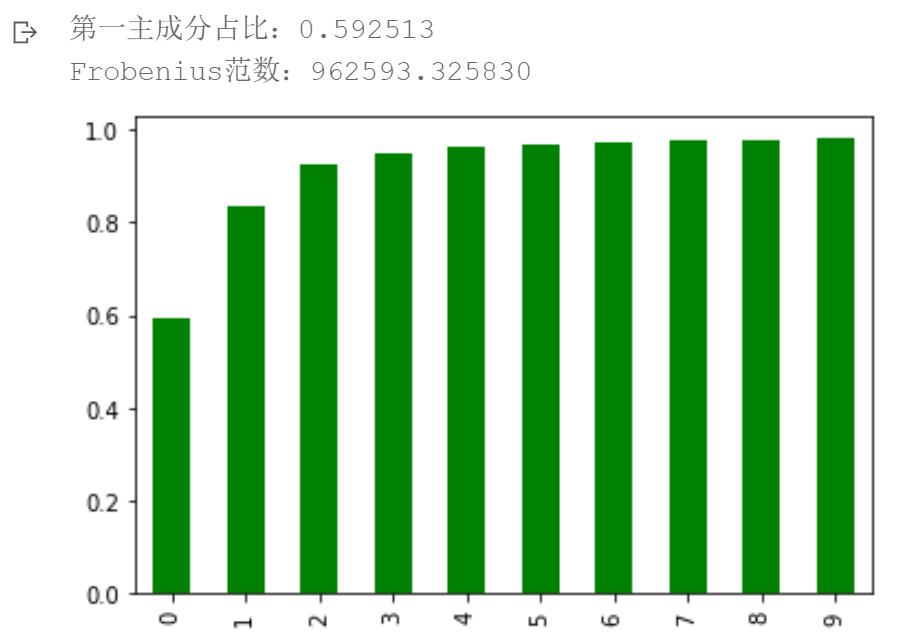
预期实验结果：（该图可以更加完善，比如，标注出横轴与纵轴的说明）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import numpy.linalg as LA
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib import font_manager
from sklearn.decomposition import PCA
from sklearn.utils.extmath import svd_flip
import numpy as np
# 画图内置到jupter环境中
%matplotlib inline 
font = font_manager.FontProperties(fname='MSYHL.TTC')
secon = pd.read_csv('secon.csv', sep=',')
secon.fillna(secon.mean(),inplace=True) # 填充均值
secon = np.mat(secon)
n_components = 590
# pca降维

lowdMat, tfMat, w, v = pca(secon, n_components=n_components)
'''
p=PCA(n_components=n_components)
lowdMat = p.fit_transform(secon)
tfMat =p.components_

print(lowdMat)
print(lowdMat.shape)
print(tfMat)
print(tfMat.shape)

w =p.explained_variance_ratio_
'''
# 计算第一主成分占比
fpc = w[0]/sum(w)
print("第一主成分占比:%f" % fpc)
# 每一个主成分的方差占比和累积方差占比计算
vp = w/sum(w)
accvp =np.cumsum(vp)

# 绘制主成分方差占比随主成分数目的变化图
# 从图可以看出，为不损失太多信息，可选择保留前6个主成分
fig = plt.figure()
plt.bar(np.arange(len(accvp[:10])),accvp[:10],0.4,color="green")
plt.title('PCA', fontproperties=font)
plt.xlabel('主成分', fontproperties=font)
plt.ylabel('主成分占比', fontproperties=font)

# 计算重构误差
meanVal = np.mean(secon, axis=0)  # 均值

#reconMat =np.mat(lowdMat)*np.mat(tfMat.T)+np.mat(meanVal)  # 重构数据
#reconMat=p.inverse_transform(lowdMat)#s重构数据

secon_centered=secon-meanVal
reconMat =np.matmul(lowdMat,tfMat.T)  # 重构数据
errMat = secon_centered-reconMat # 残差
froerr =LA.norm(errMat,'fro')  # Frobenius范数计算
print("残差的Frobenius范数：")
print(froerr)
froerrSquare =froerr*froerr
print("重建误差：残差的Frobenius范数的平方：")
print(froerrSquare)
'''
df = pd.DataFrame(lowdMat)
df.to_csv('lowdMat.csv',index= False, header= False)
df = pd.DataFrame(tfMat)
df.to_csv('tfMat.csv',index= False, header= False)
df = pd.DataFrame(reconMat)
df.to_csv('reconMat.csv',index= False, header= False)'''
#plt.show()
# 请直接运行处结果，然后提交作业，该运行结果会自动一同提交上去
第一主成分占比:0.592513
残差的Frobenius范数：
1.0674580538996893e-06
重建误差：残差的Frobenius范数的平方：
1.139466696835312e-12

"\ndf = pd.DataFrame(lowdMat)\ndf.to_csv('lowdMat.csv',index= False, header= False)\ndf = pd.DataFrame(tfMat)\ndf.to_csv('tfMat.csv',index= False, header= False)\ndf = pd.DataFrame(reconMat)\ndf.to_csv('reconMat.csv',index= False, header= False)"

output_13_2

3.6 sklearn中的PCA

任务介绍

  • 请使用sklearn中的decomposition.pca将鸢尾花数据iris映射到二维低维空间，其中X是去除标签的数据，y是标签数据
  • 请计算第一主成分的方差占比，并存为变量fpc（用于判定本题是否通过）
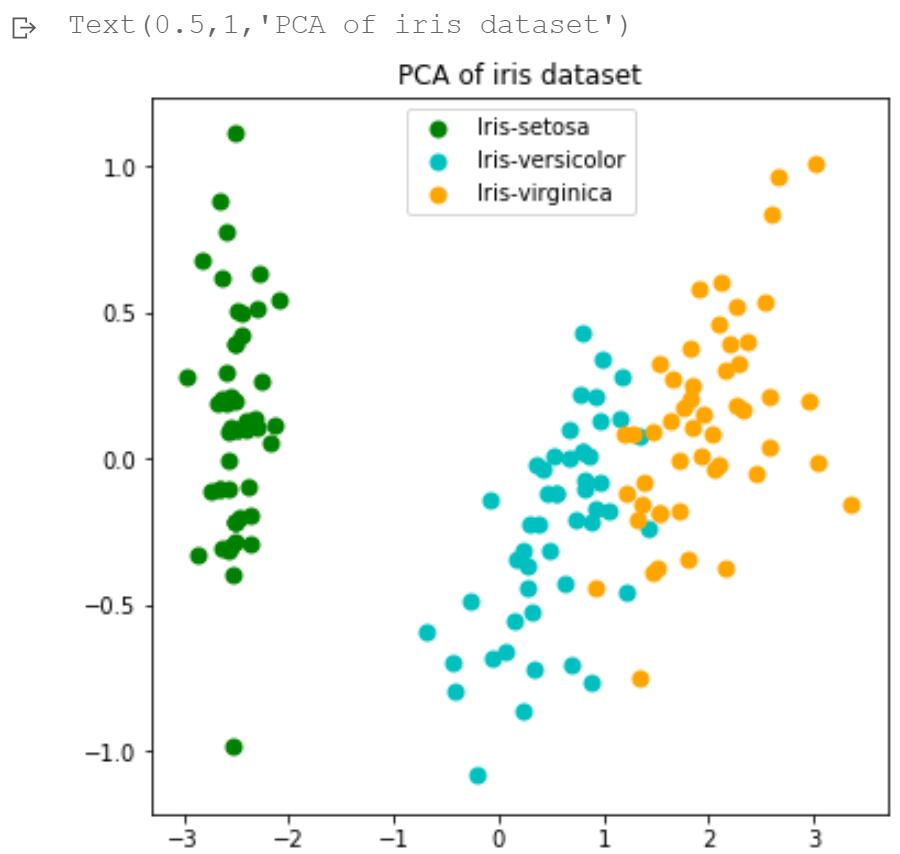
  • 请尝试绘制低维空间中不同类别数据的散点图，并分析使用其中一个主成分是否可以准确分辨不同类别？

预期实验结果

实验代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import pandas as pd
import matplotlib
%matplotlib inline
# 加载数据
iris = pd.read_csv('iris.csv', usecols=range(5))
X=iris.iloc[:,1:4]
y = iris['classes']

# pca降维过程
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 计算第一主成分方差占比
fpc =pca.explained_variance_ratio_[0]
print("第一主成分的方差占比:%f" % fpc)

# 在低维空间中绘图
colors = ['green','c','orange'] # 色系选择
f,ax = plt.subplots(figsize=(6,6))
for color, label in zip(colors, list(set(iris['classes']))):
    plt.scatter(X_pca[y == label, 0], 
                X_pca[y == label, 1],
                color=color, 
                lw=2, 
                label=label)
plt.legend(loc="upper center")
plt.title("PCA of iris dataset")


# 请直接运行处结果，然后提交作业，该运行结果会自动一同提交上去
第一主成分的方差占比:0.950872





Text(0.5,1,'PCA of iris dataset')

output_18_2

赏

谢谢你请我吃糖果

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

我很想要过这样一个温暖的冬天<br> 有一场踩起来嘎吱嘎吱的大雪<br> 有路灯下昏黄得模糊的暖光<br> 有趴在桌下酣睡的猫咪<br> 有热烘烘的烤地瓜<br> 有一壶暖胃的酒<br> 有本想看的书<br> 有窗上的雾<br> 有大毛毯<br> 还有你<br> 再见<br> 玉<br>